Research Overview

List of Research Interests

Problems:

• Finding invariance/equivariance, and Geometric Deep Learning
• Causality, and connections to model selection
• Out of distribution generalisation
• Local learning rules
• Decision making with limited data, and applications

Solutions:

• Bayesian inference and approximations to it (variational, EP, MCMC, Stein, …)
• Bayesian model selection & Neural architecture search
• Gaussian process models (deep GPs, GPSSM, GPLVM, …), practical approximations to them, and their theoretical properties
• Meta-learning
• Continual learning
• Bayesian optimisation & experiment design
• Generative modelling, semi-supervised learning, self-supervised learning
• Capsule networks
• Model-based reinforcement learning
• Connections between Bayesian inference and generalisation error bounds

High-level aims and approach

Our research aims to improve three broad properties of Machine Learning methods:

• Data efficiency: Making better predictions with less data.
• Automatic Machine Learning: Methods are too brittle, and require human design and oversight.
• Uncertainty quantification and decision making: Uncertainty tells us when risks are worth taking.

Improvements in these areas would benefit the full spectrum of applications: from tasks with small amounts of data where eliminating noise is important, to high-dimensional large-data settings where neural networks are applied to natural data like images.

Approaches from statistics can help to improve these three areas, e.g. Bayesian modelling. Bayesian modelling is well-known for helping with quantifying uncertainty. This is important for decision making, since risk needs to be taken into account. If a self-driving car is 5% sure the road ahead is blocked, it can slow down to gain more information, or perform evasive action. If a “best guess” is given of “not blocked”, the consequences can be catastrophic. Bayesian deep learning aims to get better uncertainty estimates, and we do work on this.

However, I’m more excited about an underappreciated ability of the Bayesian framework: automatic inductive bias selection. By developing this ability in neural networks, the design of network architecture could be automated. Deep learning would be much more practical if humans wouldn’t need to make a multitude of design choices, like how many layers are needed, how wide they should be, their convolutional structure, and so on. Currently, these choices are made by cross-validation, which is basically trial-and-error where different versions of the network are trained from scratch. The Bayesian approach provides a single objective function that can be optimised to find architecture and weights at the same time. The long-term goal for this line of research, is to be able to determine the connectivity structure of neurons (because this is what architecture is), in a single training run of the network. This would vastly simplify network design.

Another hypothesis in the ML community is that simply scaling models to be larger will solve the three problems mentioned above, rather than improving training procedures. Approaches like meta-learning and large language models like GPT-3 push in this direction. This brings up its own interesting open questions that statistical reasoning can contribute to: What tasks and datasets should be used? Can knowledge about the mathematics of inference inform architecture design? How should methods be evaluated? These are certainly also interesting questions to investigate.

I’m not completely sure what approach I would bet on. I certainly follow developments in meta-learning and large models carefully. If the answer to this was clear, this wouldn’t be research. Luckily, there are interesting questions to investigate in both directions.

Research Highlights

To give a more concrete idea of research we have done, here are some projects and papers roughly grouped together in themes. These projects were done together with collaborators and students, so do look at the papers themselves.

Causality & Bayesian Model Selection

This is early work, but I’m excited about it. At the NeurIPS 2022 “Causal ML for Impact” workshop we presented our paper on Causal Discovery using Marginal Likelihood. This fits within our theme of using Bayesian model selection for many things. We straightforwardly use Bayesian model selection to discover causal direction in bivariate datsets. Simple principles lead to a method that performs very well compared to existing methods.

The appeal of investigating relationships between Bayesian inference and causality is that it may provide a guide to developing methods in more complex scenarios, like causal representation learning.

(Do get in touch if you want to discuss thoughts on this work, any possible issues, or suggested benchmarks.)

Learning invariances

Invariance and equivariance are very common inductive biases, with the ubiquitous convolutional layer being the most common example. When designing architectures, humans currently choose how many convolutional layers to use, together with parameters like filter size. Often these choices are made with a laborious trial-and-error procedure (cross-validation). To make the number of choices even larger, other types of convolutional layers have been developed in recent years, which help generalisation across different scales and rotations. The optimal inductive bias varies by problem and dataset, so it would be nice if we had an automatic procedure for determining these.

We are developing methods that allow weights and architecture to be learned at the same time, by optimising a single objective function. In our paper Learning Invariances using the Marginal Likelihood we expressed invariances as data augmentations, and learned the correct data augmentation parameters through backprop with a single optimisation run. The objective function was derived from the principles of Bayesian model selection¹.

The final invariance can be visualised by looking at the samples that the data augmentation procedure generates. Samples generated for a particular input image visualise which transformations are seen as not changing the label (see figure below).

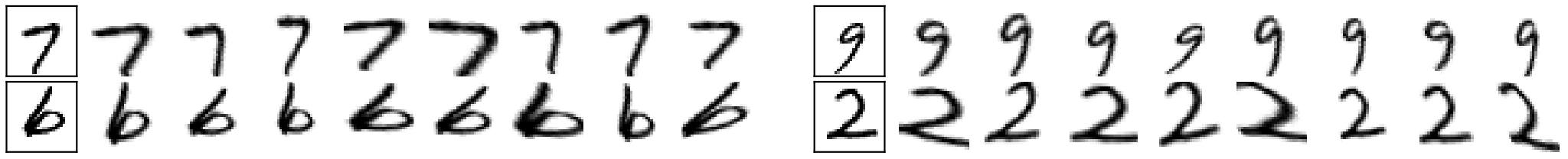
Overall, this procedure is a lot more convenient than training a model many times in a cross-validated grid search over the data augmentation parameters. What really shows that invariances are truly learned here, is that if you apply the same method to a dataset with different characteristics, a different invariance is learned. The same exact method that worked well on MNIST would learn almost full rotational invariance for rotated MNIST (see paper for results). Following the normal procedure, the cross-validated grid search would have to be performed again!

The method above was based on Gaussian processes, and we since have been working on neural network equivalents which learn different kinds of equivariant tied weights. Our 2022 UAI paper provided some nice GIFs of different kinds of convolutional structure being learned together with weights (see figure below).

What is particularly exciting is that we have been making steady progress towards making this work in deep neural networks. Approximations to the marginal likelihood that only considered the last layer were partially successful, while modifications of full-network Laplace approximations actually worked for ResNets.

What are the limitations?

• The current method is still a bit cumbersome. Our goal is to make model selection a universally applicable tool that makes hyperparameter tuning as easy as learning weights.
• You need to specify a solution space of invariances, from which the correct invariance is picked. All machine learning methods need to parameterise their solution space, but so far we have only parameterised simple ones like the space of distributions on affine transformations, and local deformations.
• We would like to be able to learn all hyperparameters that currently need to be adjusted in neural networks (e.g. how many neurons to use, or other architectural properties).

There is plenty of more to do!

Accurate and Automatic Gaussian process approximations

We also do nitty-gritty research to make Gaussian processes (a model that is also common in statistics) work really well. One neat property of GPs is that there are principles for selecting all their free parameters. In principle, this means that humans aren’t needed in the loop to train them.

Unfortunately, to reduce computational complexity, approximations need to be introduced. These often introduce free parameters again, which then means that a human has to intervene to ensure that the quality of the approximation is acceptable. This defeats part of the point! We improved two GP approximations (variational and conjugate gradient) by providing:

• automatic procedures for selecting approximation parameters, and
• mathematical guarantees on the quality of the solution.

This helps the methods give solutions in a more computationally efficient manner, while also making them more accurate. These methods help give predictions that you can really trust.

See:

• Convergence of Sparse Variational Inference in Gaussian Process Regression (or the shorter conference version)
• Tighter Bounds on the Log Marginal Likelihood of Gaussian Process Regression Using Conjugate Gradients

In the search for faster GP approximations, I have also worked on variational bounds that do not require matrix inverses to be computed. While the maths works, getting the method to optimise quickly enough for it to actually provide a practical benefit is still difficult. I do think the results are neat, and that there is a lot more to be looked into here.

Deep Gaussian processes

Why is accurate Gaussian process inference important? Well, apart from GPs being useful for noisy and/or low-data tasks where quantifying uncertainty is important², GPs are also a different representation of a neural network layer. It seems that there are advantages in terms of the quality of approximate Bayesian inference when representing a layer as a GP rather than with weights. One key research question is whether thinking about neural network layers as GPs can help bring the benefits of Bayesian inference (uncertainty and automatic model selection) to deep neural networks.

The evidence of this comes from the very first papers on deep GPs by Damianou & Lawrence, where the marginal likelihood estimate was already used for model selection. Simple inference methods keep this property, even as deep GP models become more complex.

Techniques that accomplish similar things for neural networks are only now being developed. However, in some ways the approaches in deep GPs are simpler and easier, even if they are computationally expensive. I think that there is a significant opportunity for both classes of models to benefit from each other’s strengths. Deep links between deep GPs and deep neural networks are becoming clearer, and can provide a concrete way to get the best of both worlds.

Capsules

I do believe that good model structure is the most important property for good performance. When I first heard Geoff Hinton’s talk about capsule networks, I was very intrigued by the inductive bias specified by the network alone. In addition, there seems to be a lot of probabilistic inspiration behind the routing algorithm.

Together with Lewis Smith et al, we attempted to make a fully probabilistic formulation of capsule networks, which would allow routing to be derived directly from inference. Although our practical success was limited, the project did provide a lot of insight. I do still believe in the idea behind capsules and their link to probabilistic inference. Hopefully this won’t be our last project on the topic.